6 Enzyme Kinetics
The Michaelis-Menton model of uptake rates is a well-known curve introduced in first-year biology labs. The curve arises from a simple model for a chemical reaction where a substrate \(S\) is converted to a product \(P\) through the help of an enzyme \(E\) Michaelis et al. (2011). The analysis makes use of the conservation of the enzyme and a difference of time-scales to considerably simplify the dynamics. Our analysis here is based on that of (Lin and Segel 1988, chap. 10) and (Edelstein-Keshet 1988, vol. 46, chap. 7). The diagram below is a schematic of the reaction. The enzyme binds to the substrate, forming the intermediate complex \(SE\), before converting \(S\) to \(P\) and returning to its unbound form.
Let \(s\), \(e\), \(c\) and \(p\) denote the concentrations of the substrate, enzyme, complex and product respectively. We assume that substrate and enzyme react to produce the complex at at rate \(k_1se\). This is based on the assumption of mass action, which proposes that collisions between two chemical reactants occur at a rate proportional to the product of their concentrations. The complex either decays back to separate components, which occurs at a per captia rate \(k_{-1}\), or is converted to the product releasing the enzyme, at a rate \(k_2\). The differential equations for the reaction are as follows: \[\begin{aligned} s' &= -k_1es + k_{-1}c \\ e' &= -k_1es + (k_{-1}+k_2)c \\ c' &= k_1es -(k_{-1}+k_2)c \\ p' &= k_2c \end{aligned}\]
The substrate is converted to product, which accumulates, but the enzyme is conserved in that the total concentration of enzyme plus complex is constant. This is present in the differential equations as a conservation law, \(e'+c' = 0\). Since we are interested in the case where there is initially no complex or product, \(e(t) + c(t) = e(0) = e_0\). Hence, the equations for \(s\) and \(c\) can be decoupled from the remaining two. \[\begin{aligned} s' &= -k_1(e_0-c)s + k_{-1}c, \\ c' &= k_1(e_0-c)s -(k_{-1}+k_2)c, \end{aligned} \tag{6.1}\] with the initial conditions \(s(0) = s_0\) and \(c(0) = 0\).
The two nullclines for the vector field are very similar: both are hyperbolic with horizontal asymptotes \(c = e_0\) (see Figure 6.1). The solutions we are interested in, with \(c(0) = 0\), have \(s\) initially decreasing and \(c\) increasing until the solution crosses the \(c\)-nullcline. Since \(c\) is decreasing if the solution is above the \(c\)-nullcline, the solution must follow the nullcline down to the origin.
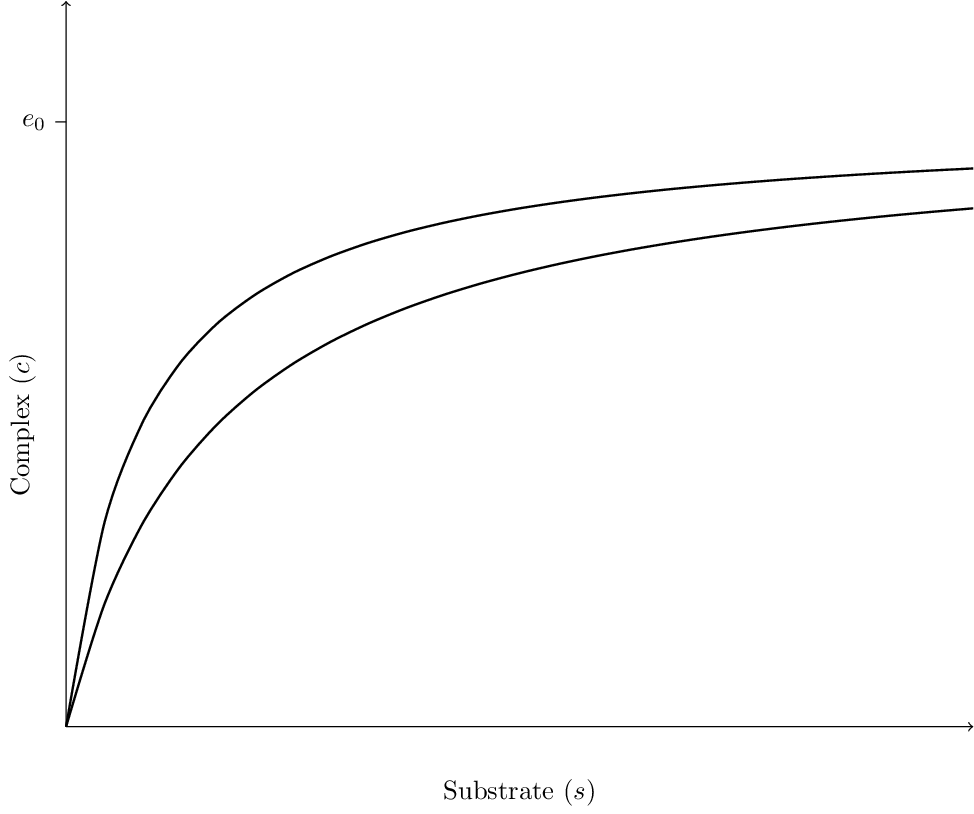
A common situation is that the concentration of substrate is large and the enzyme is mostly bound in the complex. To exploit the large ratio of substrate to enzyme, consider the rescaling \(x = s/s_0\), \(y=c/e_0\) and \(\tau = k_1e_0t\). This leads to the equations \[\begin{aligned} \frac{dx}{d\tau} &= -(1-y)x + \alpha y, \epsilon\frac{dy}{d\tau} &= (1-y)x -(\alpha+\gamma) y, \end{aligned} \tag{6.2}\] where \(\alpha = \dfrac{k_{-1}}{k_1s_0}\), \(\epsilon=\dfrac{e_0}{s_0}\) and \(\gamma=\dfrac{k_2}{k_1s_0}\). With this scaling, the assumption that the initial substrate concentration is large relative to the concentration of enzyme implies that \(\epsilon \ll 1\). As a first approximation, we can assume that the right hand side of the second equation in System 6.2 is zero. Substituting the resulting expression for \(y\) into the first equation leads to the equation \[\frac{dx}{d\tau} = -\frac{\gamma x }{\alpha+\gamma+x}.\] Thus, if the substrate concentration is large relative to that of the enzyme, then the uptake rate of substrate is approximately \(\gamma x / (\alpha + \gamma + x)\). This is the uptake rate for Michaelis-Menton kinetics.
A second time-scale for the equations found by setting \(\xi = \tau/\epsilon\). With this scaling \[\frac{dx}{d\xi} = -\epsilon(1-y)x + \epsilon\alpha y, \tag{6.3}\] \[\frac{dy}{d\xi} = (1-y)x -(\alpha+\gamma) y, \tag{6.4}\] To a first approximation, for \(\epsilon \ll 1\), we can take the right hand side of Equation 6.3 to be zero so that \(x\) is a constant. With the initial conditions \(s(0) = s_0\), \(c(0)=0\), then \(x(0)=1\) and \(y(0)=0\). Thus, assuming \(x(t) = x(0)=1\), \[\frac{dy}{d\xi} = (1-y) -(\alpha+\gamma) y.\] This is the scale for the initial rapid binding of enzyme.
Exercise 6.1 Verify that rescaling System 6.1 by introducing the new variables \(x = \dfrac{s}{s_0}\), \(y = \dfrac{c}{e_0}\), and \(\tau = k_1e_0t\) leads to System 6.2
Exercise 6.2 Write down the model for the special case \(\epsilon=0\) and verify that the initial conditions cannot be satisfied.
Exercise 6.3 Rescale Model 6.1 by introducing the new variables \(x = \dfrac{s}{s_0}\), \(y = \dfrac{c}{e_0}\), and \(\sigma = k_2t\). Use \(\epsilon = \dfrac{e_0}{s_0}\) as one of your rescaled parameters.
For easy comparison with these notes, choose \(\alpha = \dfrac{k_{-1}}{k_1s_0}\) as a second parameter. You will probably find \(\beta = k_{-1}/k_2\) a better choice for the third parameter than the \(\gamma\) used in the notes.
Exercise 6.4 Find the solution of the model obtained in Exercise 6.3 if \(\epsilon=0\). Be sure to make use of the initial conditions.